コラム
pHの近似計算について
本コラムは、工学基礎実験I「中和滴定」の補遺の「行間を埋めて」再構成したものです。pHの計算でよく近似が用いられる理由と意義についての話です。
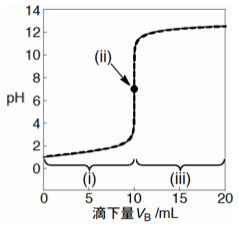 Fig. 1 強酸を強塩基で中和滴定する場合の中和滴定曲線。ただし、CA = 0.100 mol/L, 強酸の体積 VA = 10.0 mL, CB = 0.100 mol/L。実線:(i)酸性領域, (iii)酸性領域、点:(ii)当量点、破線:式(7))。
Fig. 1 強酸を強塩基で中和滴定する場合の中和滴定曲線。ただし、CA = 0.100 mol/L, 強酸の体積 VA = 10.0 mL, CB = 0.100 mol/L。実線:(i)酸性領域, (iii)酸性領域、点:(ii)当量点、破線:式(7))。
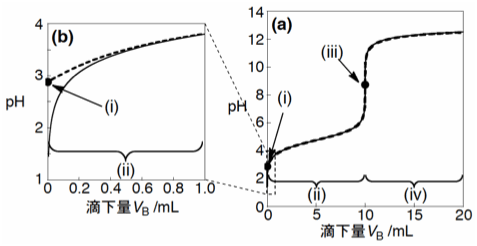
Fig. 2 弱酸を強塩基で中和滴定する場合の中和滴定曲線。ただし、pKa = 4.75, CA = 0.100 mol/L, 弱酸の体積 VA = 10.0 mL, CB = 0.100 mol/L。(a):滴下量VB = 0 – 20 mL, (b):VB = 0 – 1 mL, 点:(i)滴定前、(iii)当量点、実線:(ii)当量点前、(iv)当量点後、破線:式(7))。
高校化学や大学の分析化学の基本問題では、強酸・強塩基と弱酸・弱塩基のpHとそれらの組み合わせた中和反応が扱われます。大学の分析化学の教科書を見てみると、これらのpHを求める計算(特に弱酸・弱塩基が関わる問題)では必ずといっていいほど、適切と思われる条件式を仮定して、近似的な計算で議論が行われます。ほとんどの教科書でその考え方が記載されているので、きっとそれで実用的には問題はないのだろうと思いますが、ここでは念のために、教科書や講義ではあまり扱わない、pH計算の近似式を用いない、より厳密な解の導出について述べることにします。
例として、1価の酸HAに対して1価の塩基BOHを滴下する中和反応を考え、縦軸にpH、横軸に滴下量をとる滴定曲線を描いてみます。まず、酸HAと塩基BOHは水溶液中で電離するので、考慮すべき変数としては、[HA], [H+], [A–], [B+], [OH–], [BOH]の6種の濃度を考えることになります。この6種の濃度の間には、以下の6つの式(1)–(6)の条件式が成り立っていなければなりません。
(1)酸に関する物質収支の式
CA = [HA] + [A–] (ここで、CAはHAの分析濃度)
(2)塩基に関する物質収支の式
CB = [BOH] + [B+] (ここで、CBはBOHの分析濃度)
(3)酸解離定数
Ka = [H+][A–]/[HA]
(4)塩基解離定数
Kb = [B+][OH–]/[BOH]
(5)水のイオン積(自己プロトリシス定数)
Kw = [H+][OH–]
(6)電荷的中性に関する式
[H+] + [B+] = [A–] + [OH–]
CA = [HA] + [A–] (ここで、CAはHAの分析濃度)
(2)塩基に関する物質収支の式
CB = [BOH] + [B+] (ここで、CBはBOHの分析濃度)
(3)酸解離定数
Ka = [H+][A–]/[HA]
(4)塩基解離定数
Kb = [B+][OH–]/[BOH]
(5)水のイオン積(自己プロトリシス定数)
Kw = [H+][OH–]
(6)電荷的中性に関する式
[H+] + [B+] = [A–] + [OH–]
6個の変数に対して6つの条件式が成立しているので、HAとBOHの初期濃度、酸解離定数、塩基解離定数、水のイオン積を既知とすれば、
6変数全て決定することができます。今注目しているのはpHなので、[H+]について式をまとめてみます
(そこそこ大変ですが、がんばって導出してみましょう)。すると、
Kb[H+]4 + (KbCB + KaKb +Kw)[H+]3
+ {KaKb(CB - CA) + Kw(Ka - Kb)}[H+]2
- Kw(KaCA + KaKb + Kw)[H+]- KaKw2 = 0
・・・(7)
+ {KaKb(CB - CA) + Kw(Ka - Kb)}[H+]2
- Kw(KaCA + KaKb + Kw)[H+]- KaKw2 = 0
・・・(7)
という4次方程式が得られます。この方程式の解のうち正の実数解を選べば[H+]が求められます。この式によって、強酸–強塩基、弱酸–強塩基、強酸–強塩基、弱酸–弱塩基のどの組み合わせの場合でも滴定曲線が描けます。めでたし、めでたし、、、
ここまで書けば、なぜ分析化学の教科書でこういった議論がされないのかわかってきたと思います。それは、
(A) 式を導出したところで手計算できない。(演習や試験に出しにくい)
(B) 計算機があっても、それをわざわざ説明したくない。
(B) 計算機があっても、それをわざわざ説明したくない。
という理由があるのだと思います。さらに、下で議論しますが、
(C) 近似解がだいたい厳密解を再現できる。
(D) 近似した方が化学的に理解しやすい。
(D) 近似した方が化学的に理解しやすい。
というのが決定的です。教科書を執筆されている先生はこれが頭にあるので、わざわざ上のような議論はしないのだと思います。また、講義をする先生も実のある議論ができないので、この式をわざわざ導くことがないのでしょう。
では次に、適切な近似をおいて得られる解が式(7)からの厳密解(この方程式の解法は1年前期「微分積分」で紹介します)をどの程度再現できるか検証しておきます。
まずは、強酸を強塩基で中和する場合を例としましょう。これは、高校化学でも学習する考え方ですが、各段階で過剰な水素イオン濃度または過剰な水酸化物イオン濃度からpHを計算することで滴定曲線は描けます。式で表すと、
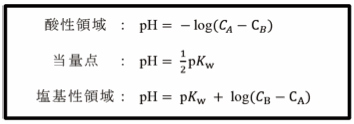 となります。これらの式と式(7)から得られる滴定曲線を比較すると、
となります。これらの式と式(7)から得られる滴定曲線を比較すると、
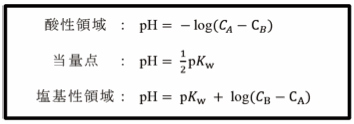 となります。これらの式と式(7)から得られる滴定曲線を比較すると、
となります。これらの式と式(7)から得られる滴定曲線を比較すると、
 Fig. 1 強酸を強塩基で中和滴定する場合の中和滴定曲線。ただし、CA = 0.100 mol/L, 強酸の体積 VA = 10.0 mL, CB = 0.100 mol/L。実線:(i)酸性領域, (iii)酸性領域、点:(ii)当量点、破線:式(7))。
Fig. 1 強酸を強塩基で中和滴定する場合の中和滴定曲線。ただし、CA = 0.100 mol/L, 強酸の体積 VA = 10.0 mL, CB = 0.100 mol/L。実線:(i)酸性領域, (iii)酸性領域、点:(ii)当量点、破線:式(7))。
Fig. 1からわかるように、両方の曲線は全領域にわたってよく一致しています。このことから、強酸と強塩基との中和反応については、上の3つの簡単な近似式で議論しても問題ないようです。
もう一つの例として、弱酸を強塩基で中和する場合を考えましょう。これも高校化学の発展問題として、また大学では分析化学の範囲で学習する内容ですが、弱酸と強塩基の滴定に関しては、滴定前、当量点前、当量点、当量点後に分けて考える近似法がよく用いられます。
(i)滴定前:弱酸HAはあまり電離していないと考える
CA = [HA] + [A–] ~ [HA]
(ii)当量点前:加えた塩基の分だけHAが消費(中和)され、A–が生成
[HA] = CA - CB
[A–] = CB
(iii)当量点:共役塩基A–が塩基として働き、わずかにHAとOH–を生成
CA = [HA] + [A–] ~ [A–]
[HA] = [OH–]
(iv)当量点後:当量点以降加えた塩基の分だけOH–が溶液中に存在
[OH–] = CB - CA
CA = [HA] + [A–] ~ [HA]
(ii)当量点前:加えた塩基の分だけHAが消費(中和)され、A–が生成
[HA] = CA - CB
[A–] = CB
(iii)当量点:共役塩基A–が塩基として働き、わずかにHAとOH–を生成
CA = [HA] + [A–] ~ [A–]
[HA] = [OH–]
(iv)当量点後:当量点以降加えた塩基の分だけOH–が溶液中に存在
[OH–] = CB - CA
これらの近似式から下の式が導かれます。
 これらの式と式(7)から得られる滴定曲線を比較します(Fig. 2)。
これらの式と式(7)から得られる滴定曲線を比較します(Fig. 2)。
 これらの式と式(7)から得られる滴定曲線を比較します(Fig. 2)。
これらの式と式(7)から得られる滴定曲線を比較します(Fig. 2)。

Fig. 2 弱酸を強塩基で中和滴定する場合の中和滴定曲線。ただし、pKa = 4.75, CA = 0.100 mol/L, 弱酸の体積 VA = 10.0 mL, CB = 0.100 mol/L。(a):滴下量VB = 0 – 20 mL, (b):VB = 0 – 1 mL, 点:(i)滴定前、(iii)当量点、実線:(ii)当量点前、(iv)当量点後、破線:式(7))。
この場合、滴定初期の近似はあまり良くありませんが、両方の曲線はほとんどの領域で一致しています。
ここでは2例しか挙げていませんが、高校化学や大学の分析化学の教科書で扱われる近似法は、一般的な酸・塩基溶液のpHを簡単に見積もるのには十分です(極端に濃度がうすい等の条件がある場合は別ですが)。むしろ、厳密に解こうとするよりも、上の(i)-(iv)で考えたように、「中和の各段階でどの化学種が主に存在し、どの種がほとんど存在しないのか」という点に注目することの方が、化学的(分子論的)な感覚を養う上で効果的だと思います。
とはいえ、厳密な解を求める術を捨ててはいけません。なぜならば、その近似が妥当なものであるかどうかは、厳密解を求められてはじめて議論できることだからです。この中和滴定の例に限らず、化学ではいろんな場面で近似法がよく用いられます。厳密解と近似解、両方それぞれに重要な概念・考え方が隠されているはずですので、その点に注意してみてください。